The technique to represent and work with numbers is called number system. Decimal number system is the most common number system. Other popular number systems include binary number system, octal number system, hexadecimal number system, etc.
Decimal Number System
Decimal number system is a base 10 number system having 10 digits from 0 to 9. This means that any numerical quantity can be represented using these 10 digits. Decimal number system is also a positional value system. This means that the value of digits will depend on its position. Let us take an example to understand this.
Say we have three numbers – 734, 971 and 207. The value of 7 in all three numbers is different−
- In 734, value of 7 is 7 hundreds or 700 or 7 × 100 or 7 × 102
- In 971, value of 7 is 7 tens or 70 or 7 × 10 or 7 × 101
- In 207, value 0f 7 is 7 units or 7 or 7 × 1 or 7 × 100
The weightage of each position can be represented as follows −

In digital systems, instructions are given through electric signals; variation is done by varying the voltage of the signal. Having 10 different voltages to implement decimal number system in digital equipment is difficult. So, many number systems that are easier to implement digitally have been developed. Let’s look at them in detail.
Binary Number System
The easiest way to vary instructions through electric signals is two-state system – on and off. On is represented as 1 and off as 0, though 0 is not actually no signal but signal at a lower voltage. The number system having just these two digits – 0 and 1 – is called binary number system.
Each binary digit is also called a bit. Binary number system is also positional value system, where each digit has a value expressed in powers of 2, as displayed here.

In any binary number, the rightmost digit is called least significant bit (LSB) and leftmost digit is called most significant bit (MSB).
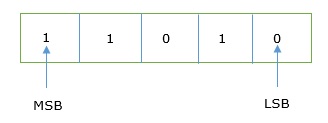
And decimal equivalent of this number is sum of product of each digit with its positional value.
110102 = 1×24 + 1×23 + 0×22 + 1×21 + 0×20
= 16 + 8 + 0 + 2 + 0
= 2610
Computer memory is measured in terms of how many bits it can store. Here is a chart for memory capacity conversion.
- 1 byte (B) = 8 bits
- 1 Kilobytes (KB) = 1024 bytes
- 1 Megabyte (MB) = 1024 KB
- 1 Gigabyte (GB) = 1024 MB
- 1 Terabyte (TB) = 1024 GB
- 1 Exabyte (EB) = 1024 PB
- 1 Zettabyte = 1024 EB
- 1 Yottabyte (YB) = 1024 ZB
Octal Number System
Octal number system has eight digits – 0, 1, 2, 3, 4, 5, 6 and 7. Octal number system is also a positional value system with where each digit has its value expressed in powers of 8, as shown here −

Decimal equivalent of any octal number is sum of product of each digit with its positional value.
7268 = 7×82 + 2×81 + 6×80
= 448 + 16 + 6
= 47010
Hexadecimal Number System
Octal number system has 16 symbols – 0 to 9 and A to F where A is equal to 10, B is equal to 11 and so on till F. Hexadecimal number system is also a positional value system with where each digit has its value expressed in powers of 16, as shown here −

Decimal equivalent of any hexadecimal number is sum of product of each digit with its positional value.
27FB16 = 2×163 + 7×162 + 15×161 + 10×160
= 8192 + 1792 + 240 +10
= 1023410
Number System Relationship
The following table depicts the relationship between decimal, binary, octal and hexadecimal number systems.
| HEXADECIMAL | DECIMAL | OCTAL | BINARY |
|---|---|---|---|
| 0 | 0 | 0 | 0000 |
| 1 | 1 | 1 | 0001 |
| 2 | 2 | 2 | 0010 |
| 3 | 3 | 3 | 0011 |
| 4 | 4 | 4 | 0100 |
| 5 | 5 | 5 | 0101 |
| 6 | 6 | 6 | 0110 |
| 7 | 7 | 7 | 0111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| A | 10 | 12 | 1010 |
| B | 11 | 13 | 1011 |
| C | 12 | 14 | 1100 |
| D | 13 | 15 | 1101 |
| E | 14 | 16 | 1110 |
| F | 15 | 17 | 1111 |
